A Bayesian approach to decision making in early development clinical trials: phase1b R package

NS&IBGH Scientific Knowledge Sharing Meeting

Audrey Yeo

Novartis Headquartes

Introduction



Introduction



Early development trials and why phase1b?

Objectives

  • introduce Beta Binomial model
  • explore postprob and predprob
  • explore simulation studies using ocPostprob
  • question and answer


The Posterior Construction

\[ {P( B | A)} = { {P(A|B)P(B)} \over {P(A) } } \]

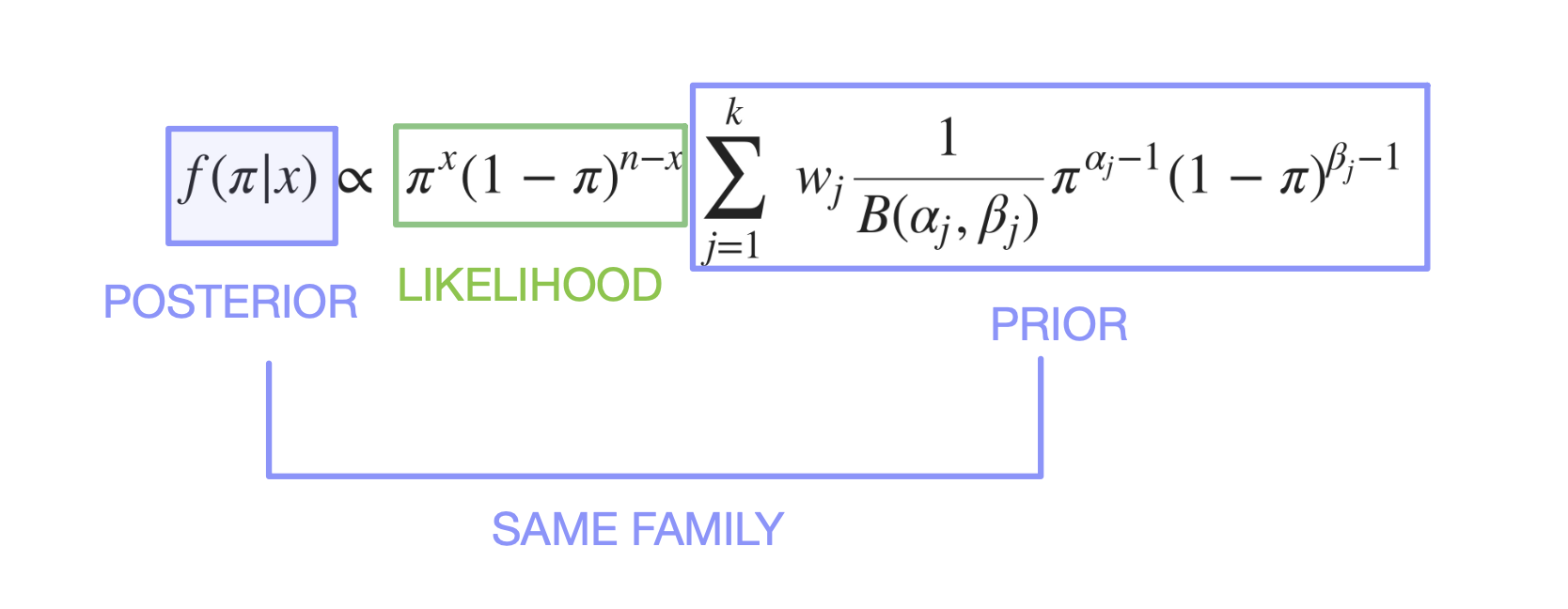
Beta Prior is a conjugate to the Posterior. Merriam-Webster Dictionary on “conjugate” : coupled, connected, or related.

Prior and Posterior of Beta Distribution for response rate

  • Conjugate Prior is \(f(\pi)\), where \(\pi \sim {Beta(\alpha, \beta)}\), same family of distribution of Posterior (see below)

  • We know the mean response rate (RR) is : \[\pi = \ \frac {\alpha}{\alpha + \beta}\]

  • Likelihood is \(f(x|\pi)\), where \(x \sim {Binomial(x, n)}\)

  • The updated Posterior \(f( \pi | x )\) is again a \(Beta\) distribution (same family as prior) : \[ \pi| \ x \sim Beta(\alpha + x, \ \beta + n - x)\] where \(x\) is the number of responders of current trials

Detour : Polack et al (2020), Phase III trial

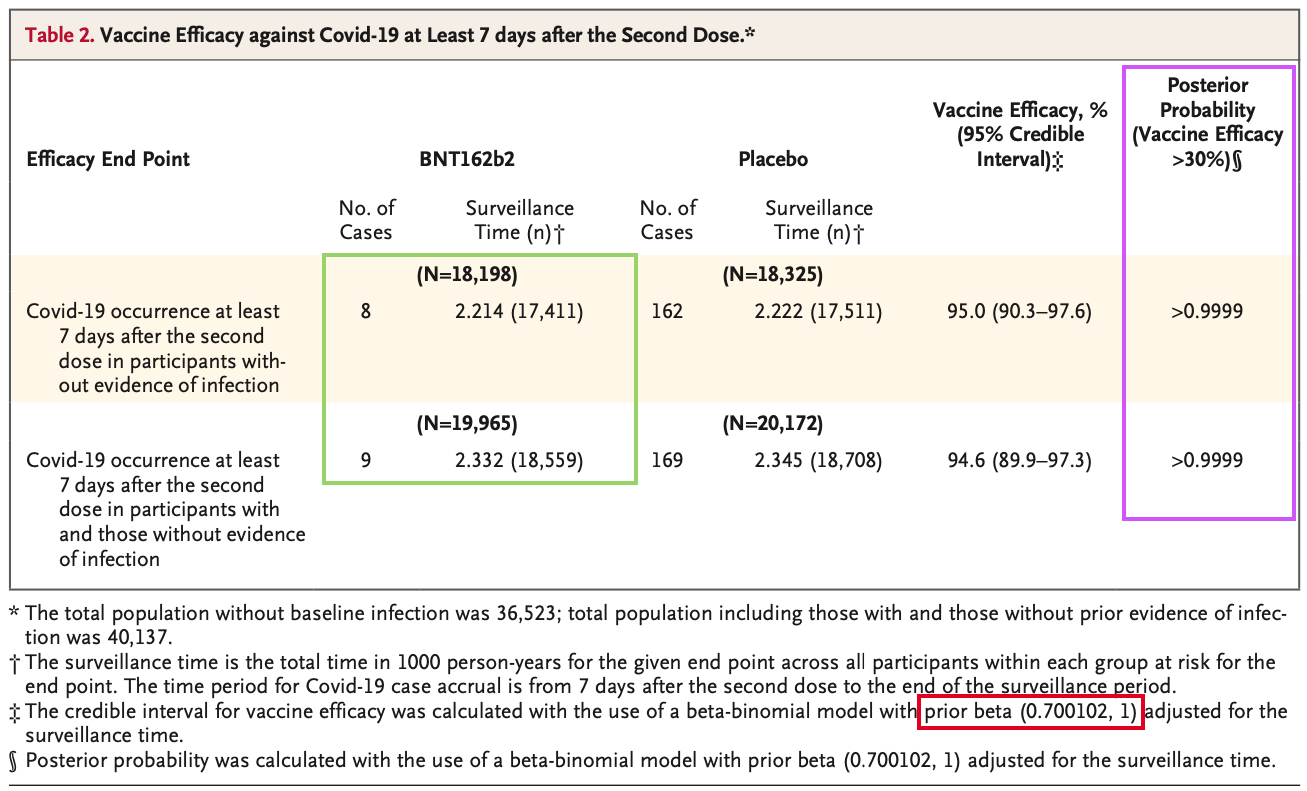
Beta Prior and Mean for BNT162b2 Phase III :

History and how to install :

  • 2015 : Started as a need in Roche’s early development group, package development led by Daniel Sabanés Bové in 2015.

  • 2023 : Refactoring, Renaming, adding Unit and Integration tests as current State-of-Art Software Engineering practice.

  • 2025 : CRAN submission is anticipated

  • 100% written in R and Open Source.

  • website : genentech.github.io/phase1b/

library(devtools)
devtools::install_github("https://github.com/Genentech/phase1b")
library(phase1b)

Use case:

A single arm novel therapeutic with an assumed control response rate is at most 60%
Example Interim Final
Responders 16 23
n 23 40
Response rate 69.57 % 57.5 %
Posterior probability* ask phase1b ask phase1b
Predictive posterior probability* ask phase1b -
Decision to develop molecule further : Go/Stop/Grey Zone ask phase1b ask phase1b



* Posterior Probability : \(P (\pi > 60 \% | \alpha + x, \beta + n - x )\)
* Predictive Posterior Probability : \(P (success \ or \ failure \ at \ final)\)

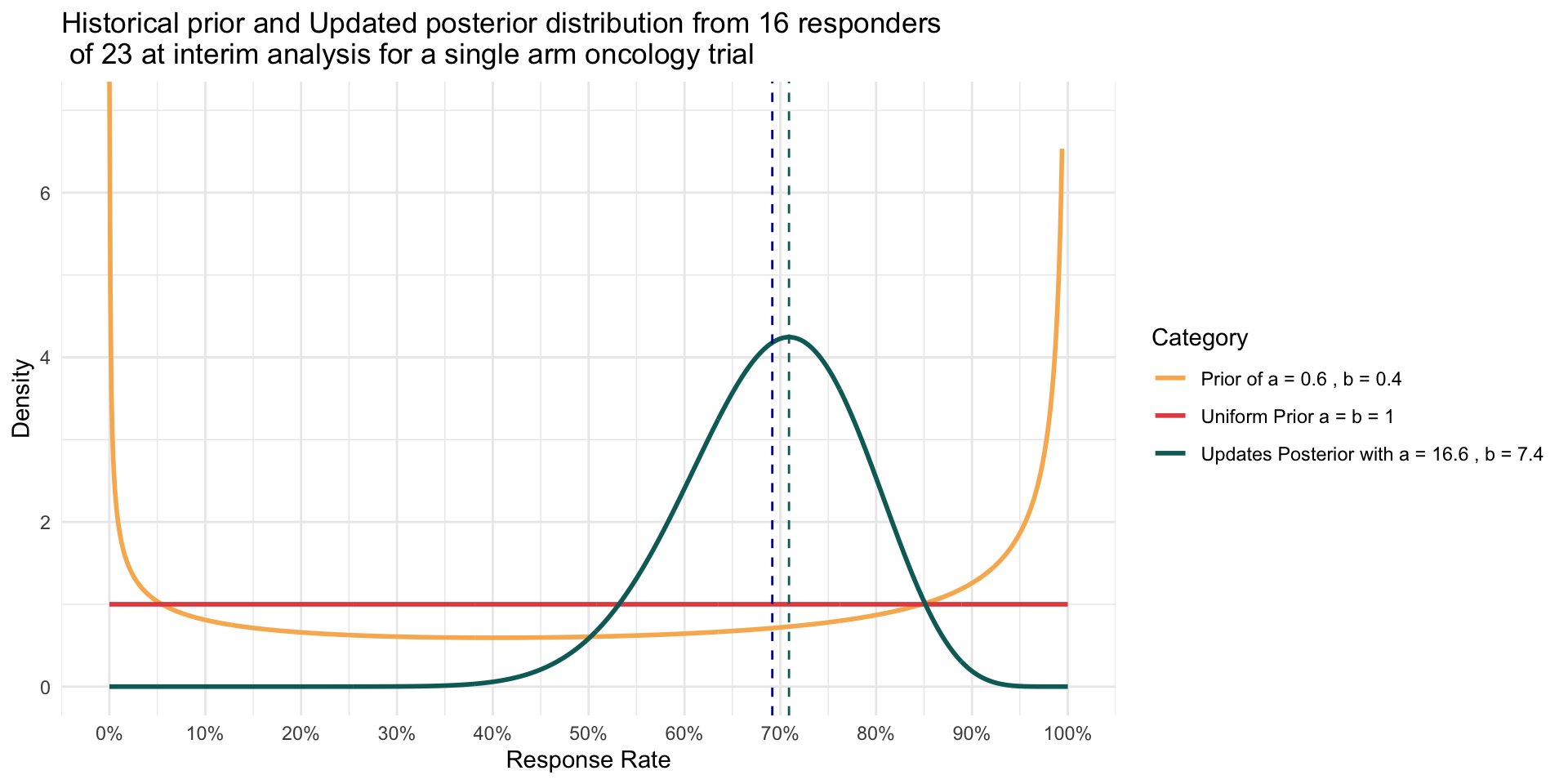
Updating the Posterior

  • Using the formula for the mean, where \(\alpha = 0.6, \beta = 0.4\) and at interim x = 16, n = 23 : \[ \pi = \ \frac {\alpha}{\alpha + \beta} = \ \frac {\alpha_{updated} }{\alpha_{updated} + \beta_{updated}} = \ \frac {16.6 }{16.6 + 7.4} ≈ 69.17 \% \]

    \[ mode (\pi) = \ \frac {\alpha_{updated} -1 }{\alpha_{updated} + \beta_{updated} - 2} = \ \frac {16.6 -1 }{16.6 + 7.4 - 2} ≈ 70.90 \% \]

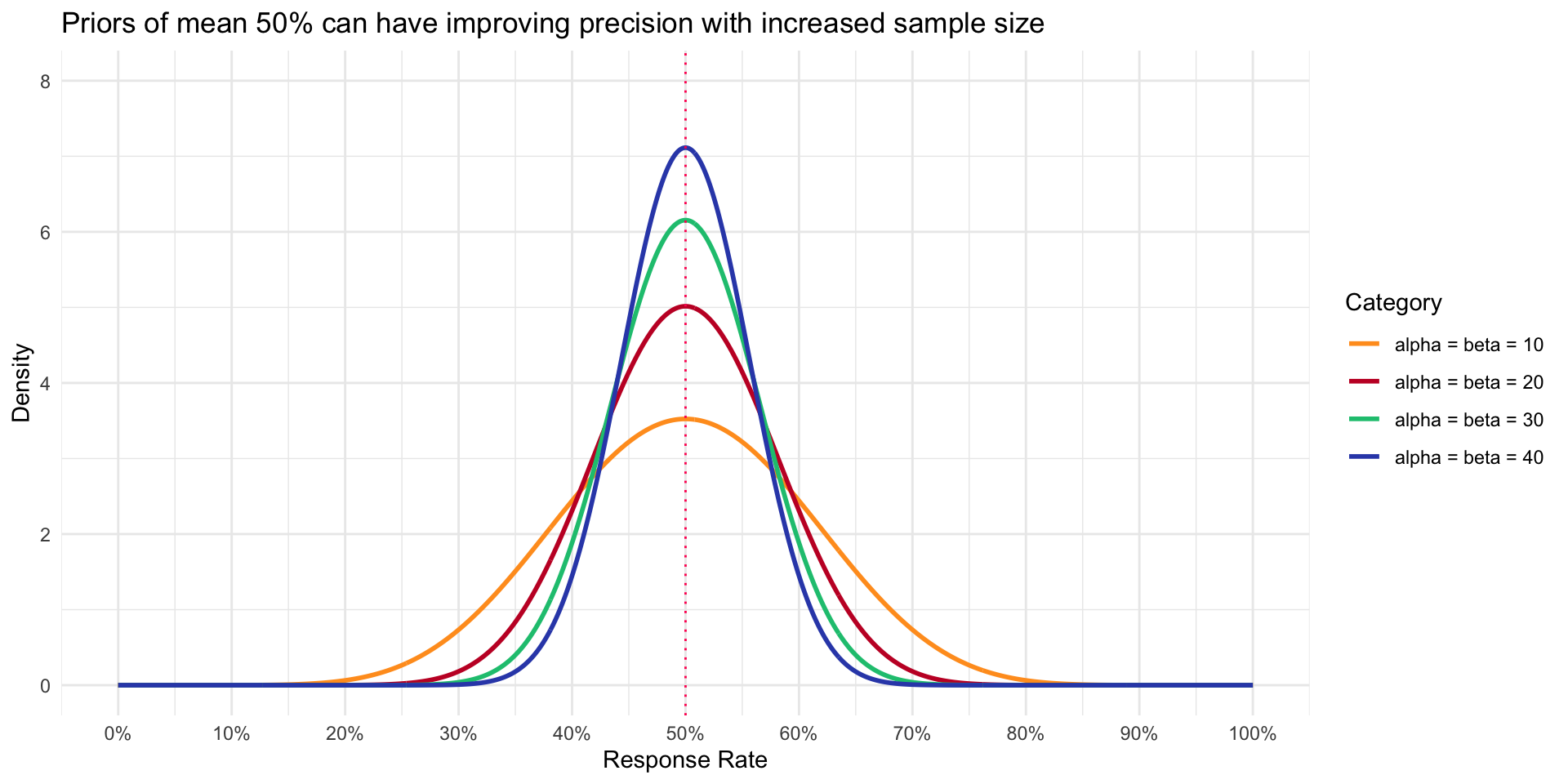
A variety of Priors

  • To illustrate how density of Prior changes with increased sample size even though mean is the same
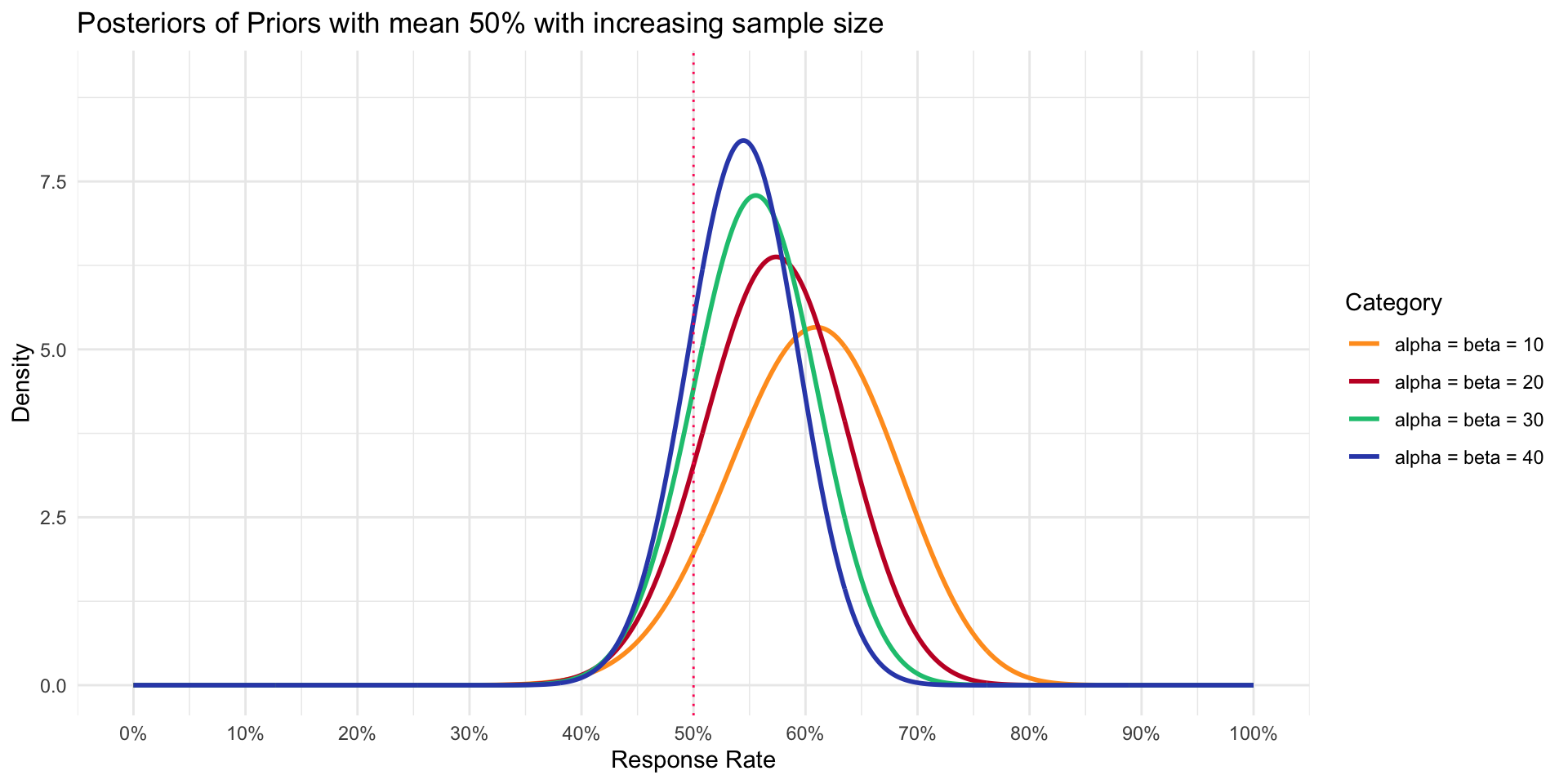
This plot shows how the priors of mean 50% can have improving precision with increased sample size.

A variety of Posteriors with “different” data

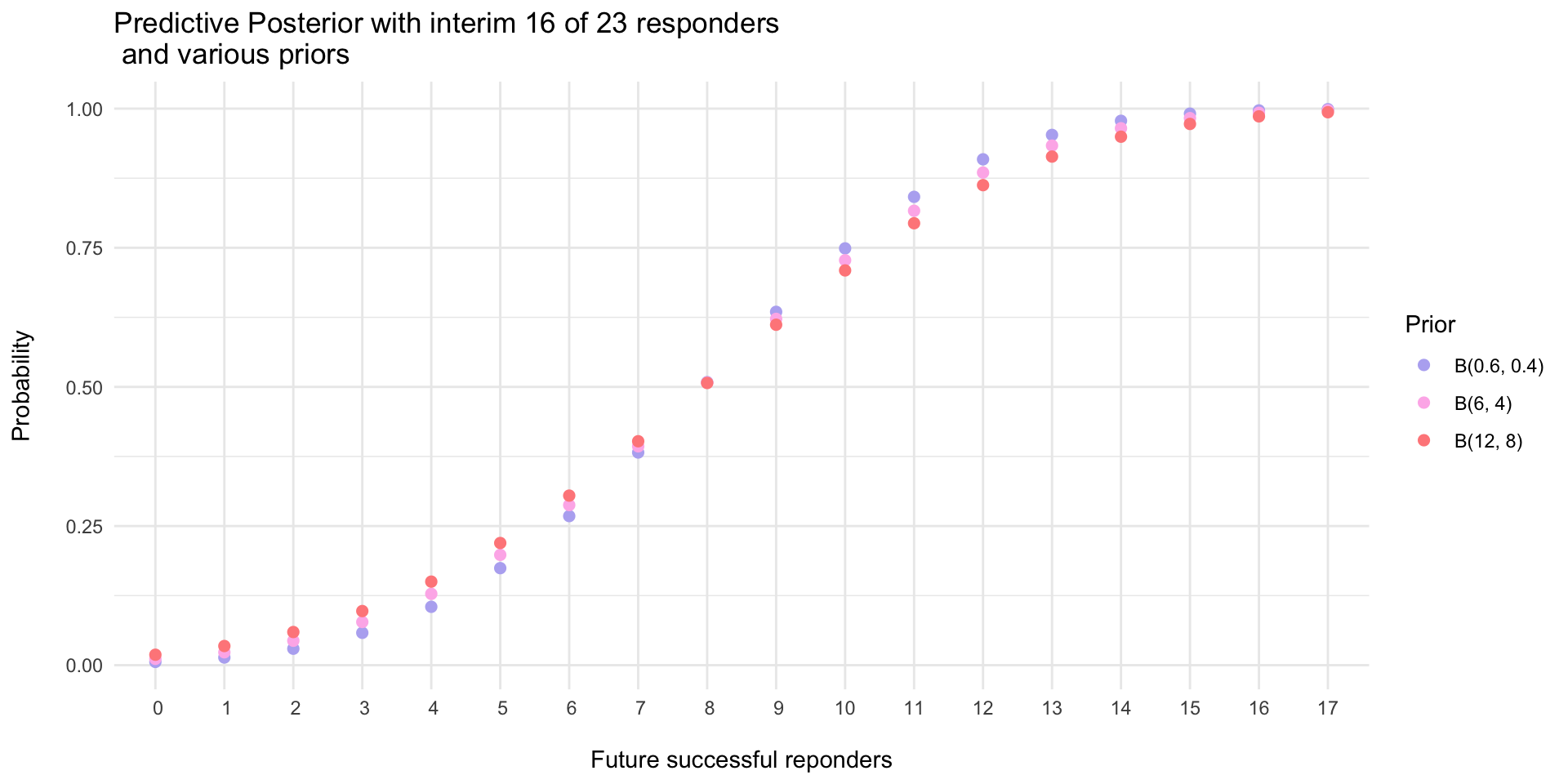
  • Data showed 16 of 23 responders (~69% response rate)
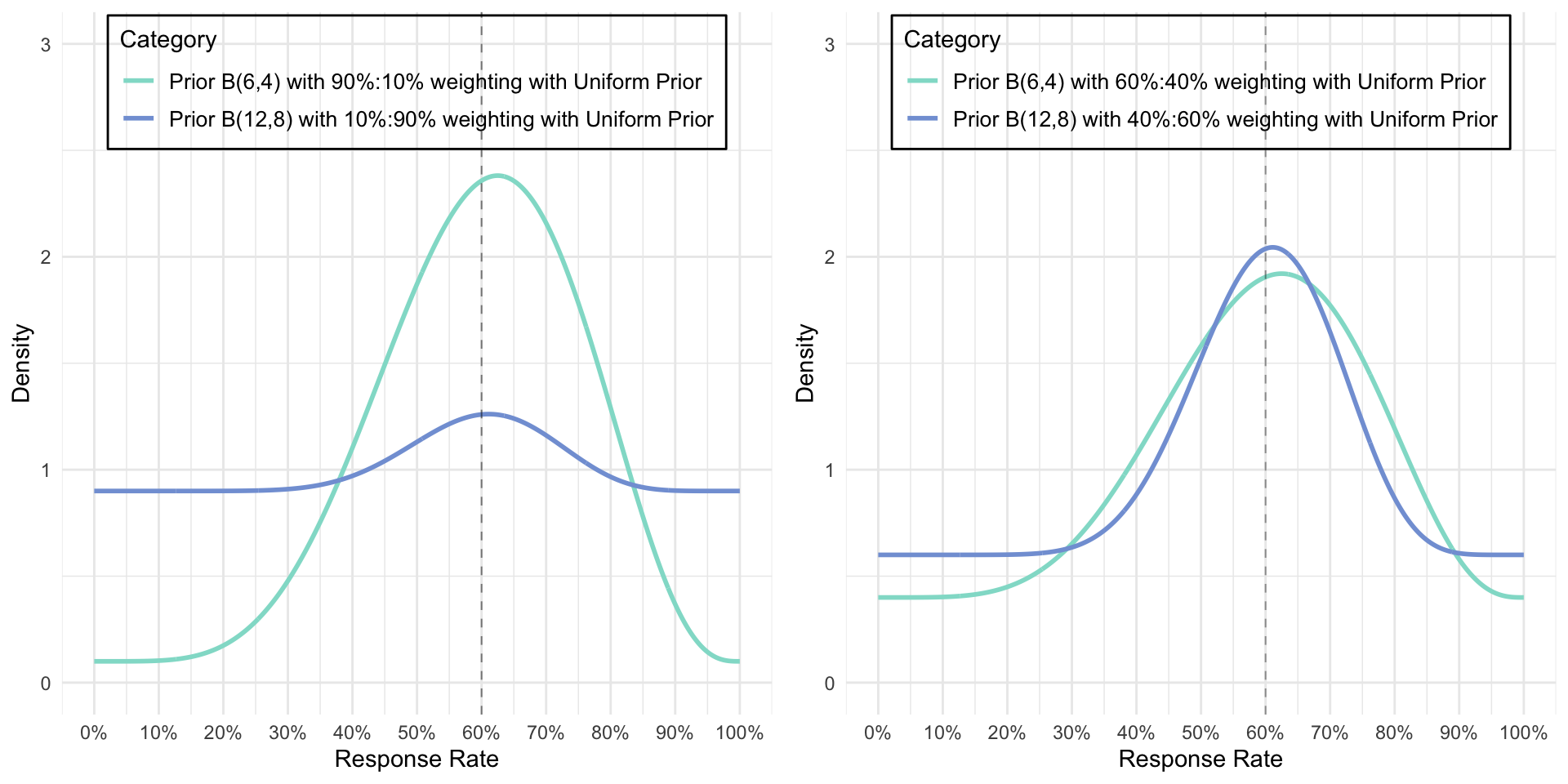
This plot shows how the priors of mean 50% can have improving precision with increased sample size.

Effect of weights (and beta Mixtures)

Terminology

  • A “look” is a stop
  • A stop is when a rule is applied
  • The rule is specified for Go, Stop or Evaluate (Gray zone)
  • If the rule is met, the result is Go, Stop or Evaluate (Gray zone)
  • Rules are applied at interim or final
  • Go = Success = Efficacious
  • Stop = Failure = Futile
  • Rule = Criteria, e.g. Go rule is a Go Criteria

postprob() example (Lee & Liu, 2008)

Example Interim
Responders 16
n 23
Response rate 69.57 %
Standard of Care Response rate 60 %
Posterior probability postprob( ) call from phase1b 
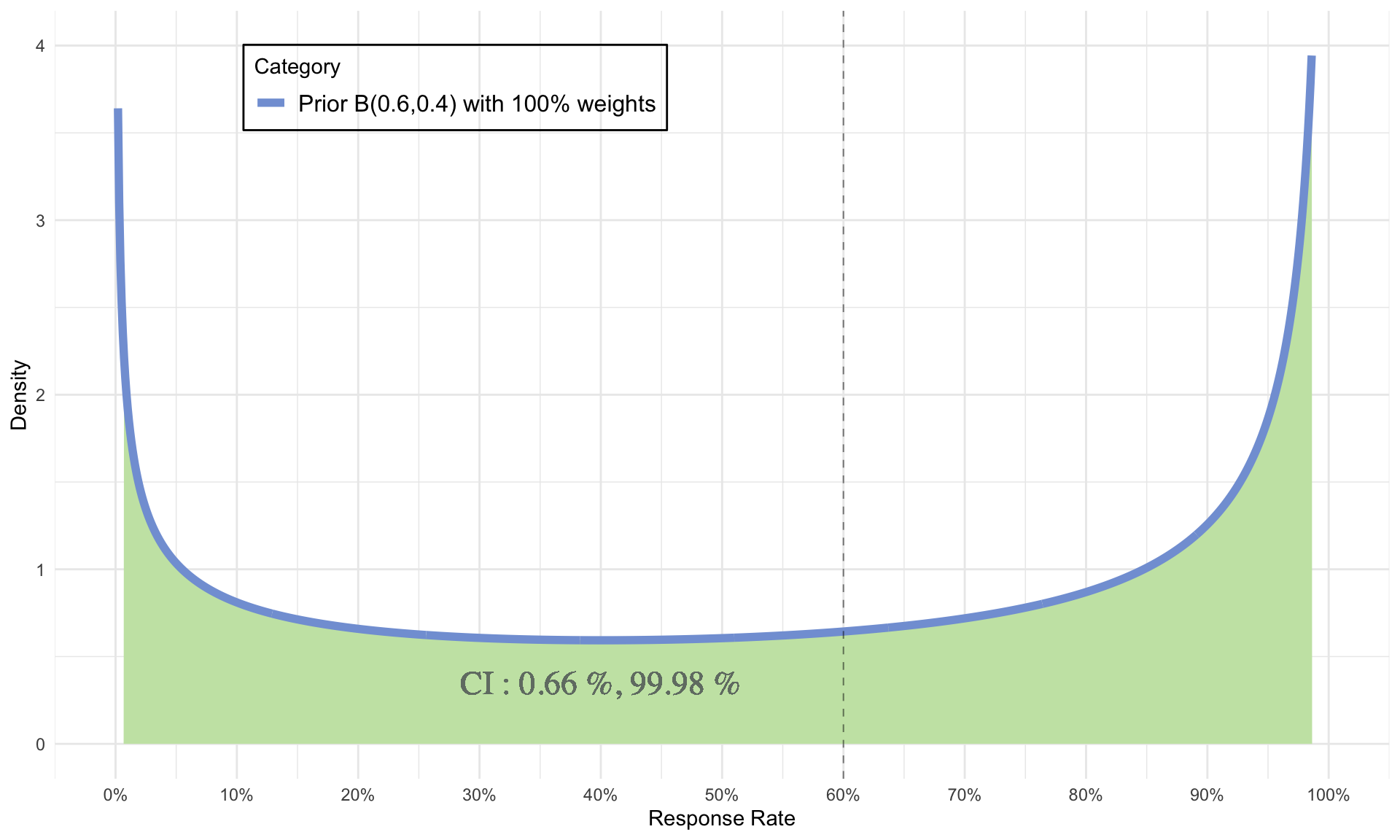
phase1b::postprob(x = 16, n = 23, p = 0.60, par = c(0.6, 0.4))
[1] 0.8359808

Choice of Weak Priors



  • \(\alpha\) = 0.6 = number of responses
  • \(\beta\) = 0.4 = number of non-responses
  • \(\alpha + \beta\) = 1 = sample size
  • \(\mu = 60 \%, CI = 0.66 \% \ and \ 99.98 \%\)

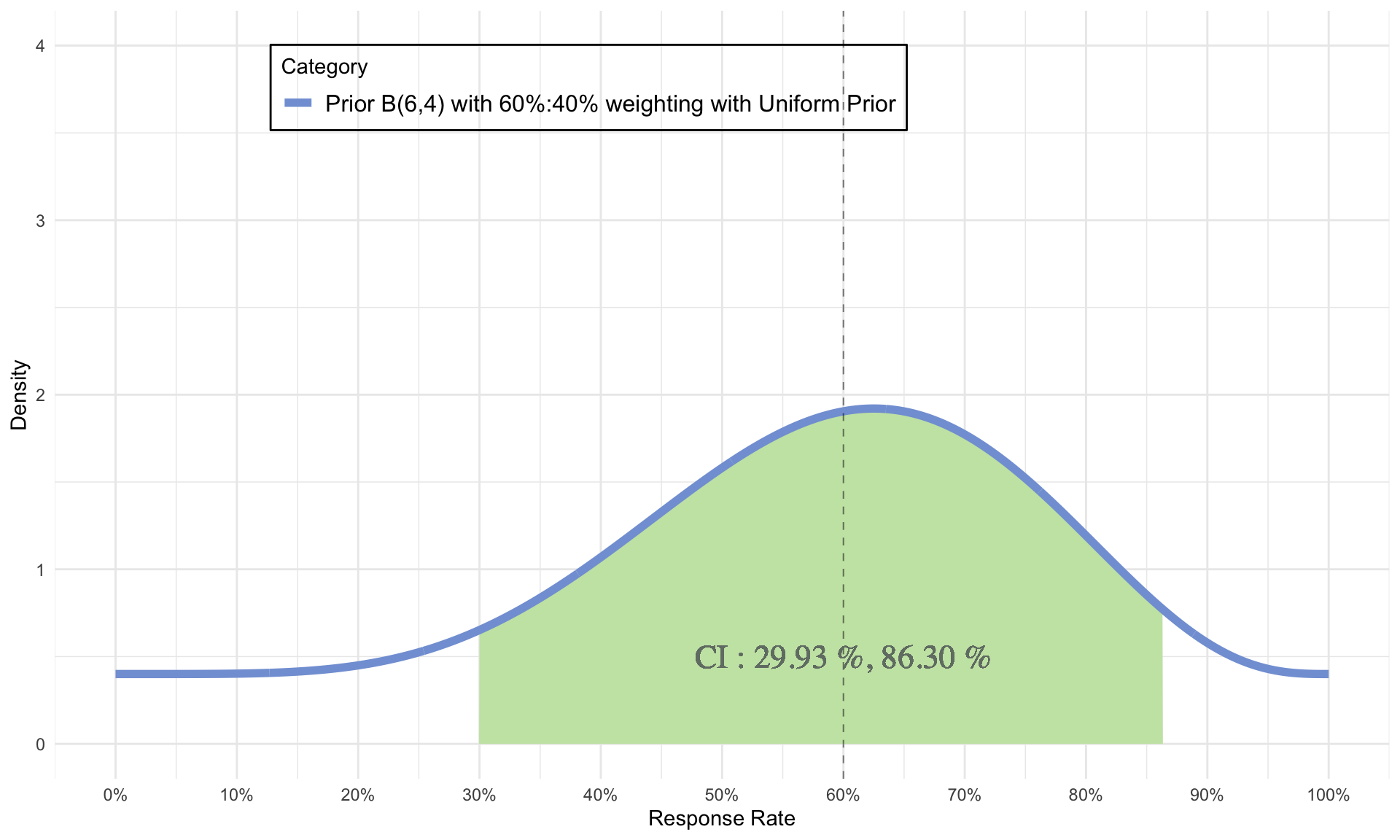
Choice of Stronger Priors



  • \(\alpha\) = 6 = number of responses
  • \(\beta\) = 4 = number of non-responses
  • \(\alpha + \beta\) = 10 = sample size
  • \(\mu = 60 \%, CI = 29.93 \% \ and \ 86.30 \%\)

Posterior results with varying Priors

Example Interim
Responders 16
n 23
Response rate 69.57 %
Standard of Care Response rate 60 %
Posterior probability postprob( ) call from phase1b 
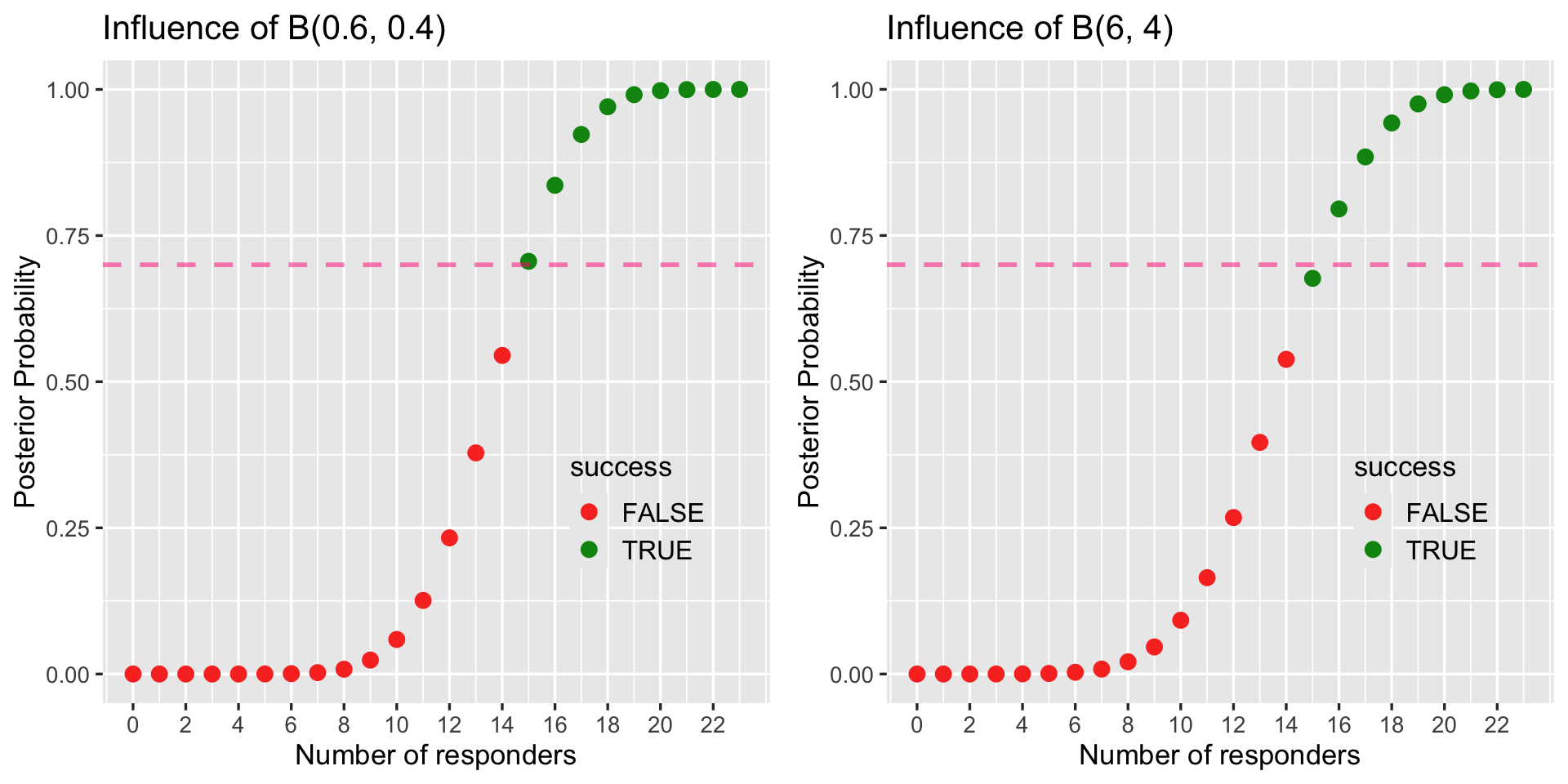
weaker_prior <- phase1b::postprob(x = 16, n = 23, p = 0.60, par = c(0.6, 0.4))

stronger_prior <- phase1b::postprob(x = 16, n = 23, p = 0.60, par = c(6, 4))

print(paste0("postprob of Weaker prior = ", round(weaker_prior, digits = 4), " and postprob of Stronger prior = ", round(stronger_prior, digits = 4)))
[1] "postprob of Weaker prior = 0.836 and postprob of Stronger prior = 0.7954"

Posterior Probability

  • Interim trial is efficacious if posterior probability exceeds 70% or P( RR ≥ 60 % | data ) > 70%
This graphs side by side show that by increasing number of responders out of 23 reaches our TPP threshold
Figure 1

Beta prior mixture

  • phase1b facilitates the flexibility of usingvarious priors and its respective weightings:

               Prior is P_E ~ sum(weights * beta(parE[, 1], parE[, 2]))
a = phase1b::postprob(x = 16,
             n = 23,
             p = 0.60,
             parE = c(0.6, 0.4), weights = 1)

b = phase1b::postprob(x = 16,
             n = 23,
             p = 0.60,
             parE = c(2, 4), weights = 1)

0.5*(a + b)

phase1b::postprob(x = 16,
             n = 23,
             p = 0.60,
             parE = rbind(c(0.6, 0.4), c(2, 4)), weights = c(0.5, 0.5))
  • Posterior formulation :

\[ f(\pi | x) \propto \ \pi^{x} (1-\pi)^{n-x}\sum_{j = 1}^{k} \ w_j \frac {1}{B(\alpha_j, \beta_j)} \pi^{\alpha_j-1}(1-\pi)^{\beta_j-1} \]

predprob() example (Lee & Liu, 2008)

Example Interim
Responders 16
n 23
Response rate 69.57 %
Standard of Care Response rate 60 %
Predictive Posterior probability predprob( ) call from phase1b 
control = 0.6
confidence_seventy = 0.7
result <- phase1b::predprob(
  x = 16, n = 23, Nmax = 40, p = control, thetaT = confidence_seventy,
  parE = c(0.6, 0.4)
)
result$result
[1] 0.8211011
confidence_ninety = 0.9
result_high_thetaT <- phase1b::predprob(
  x = 16, n = 23, Nmax = 40, p = control, thetaT = confidence_ninety,
  parE = c(0.6, 0.4)
)
result_high_thetaT$result
[1] 0.5655589

Predictive Posterior Probability

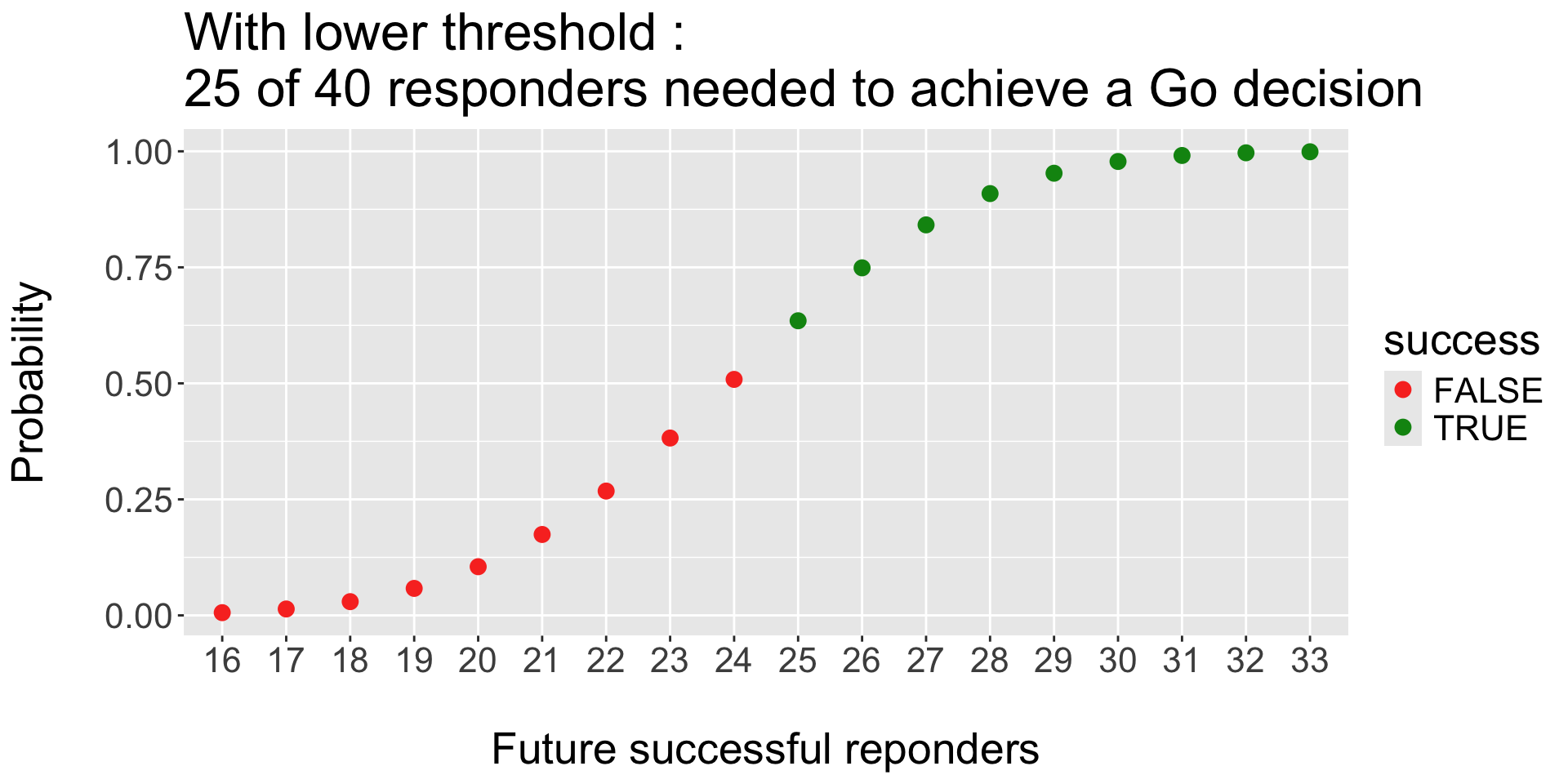
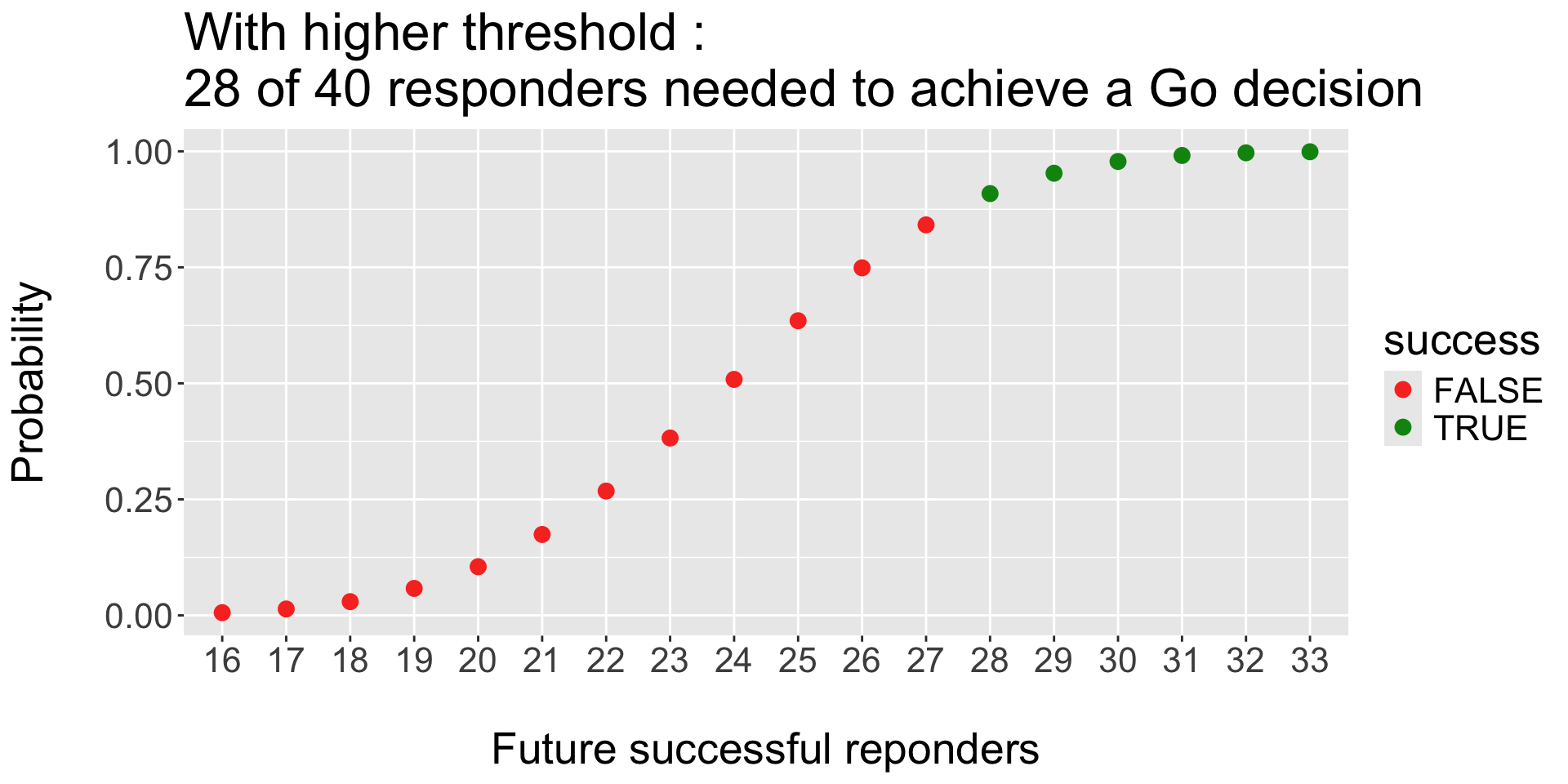
These two graphs side by side show that by increasing the threshold for an Efficacy or Go decision, the number of responders out of 40 is higher with the higher threshold, ie 35 patients instead of 32 patients of 40
(a) \(P (\pi > 0.6 | \ data )\) > 70%
These two graphs side by side show that by increasing the threshold for an Efficacy or Go decision, the number of responders out of 40 is higher with the higher threshold, ie 35 patients instead of 32 patients of 40
(b) \(P (\pi > 0.6 | \ data )\) > 90%
Figure 2: Predictive Posterior CDF for different Efficacy Rules

Operating Characteristics : threshold for Success (and failure):

  • Efficacy criteria, e.g. we would stop for Efficacy if :

Pr( RR > p1) > tU

  • Futility criteria, eg. we would stop for Futility if :

Pr( RR < p0) > tL

Rules and Operating characteristics. A use case for ocPostprob():

  • Look for Efficacy: Go if \(P( \pi > 60\% | \ data ) > 90 \%\)
  • Look for Futility: Stop if \(P( \pi < 60\% | \ data ) > 70 \%\)
  • Prior of treatment arm \(Beta(0.6, 0.4)\).
set.seed(2025)
res <- phase1b::ocPostprob(
  nnE = c(23, 40), truep = 0.60, p0 = 0.60, p1 = 0.69, tL = 0.70, tU = 0.90, parE = c(0.6, 0.4),
  sim = 500, wiggle = TRUE, nnF = c(23, 40)
)
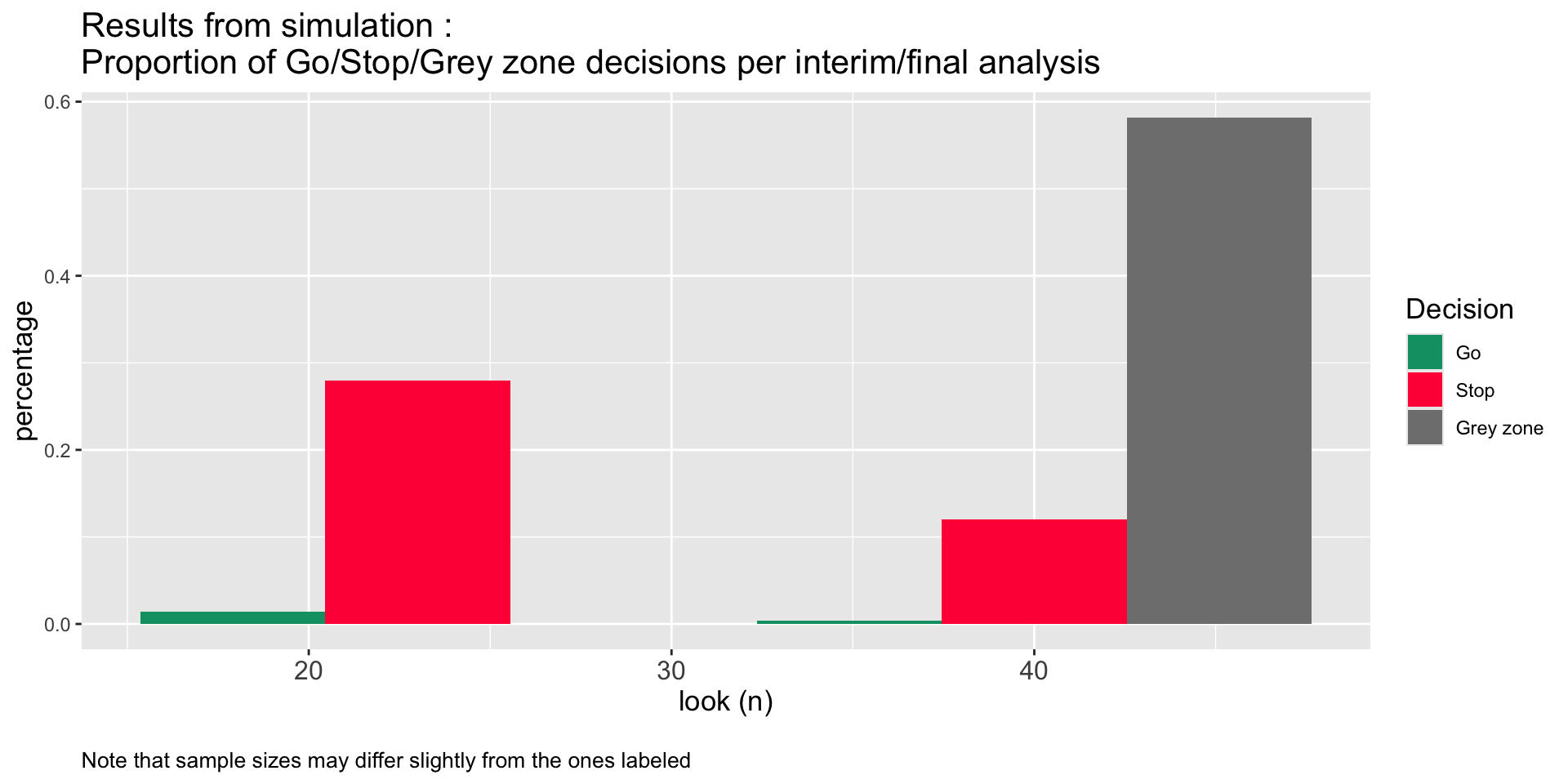
res$oc
  ExpectedN PrStopEarly PrEarlyEff PrEarlyFut PrEfficacy PrFutility PrGrayZone
1    35.182       0.294      0.014       0.28      0.018        0.4      0.582

Plotting results form ocPostprob()

plotOc0(
  decision = res$Decision,
  all_sizes = res$SampleSize,
  all_looks = res$Looks,
  wiggle_status = res$params$wiggle
)

Expanded features

…. and wiggle room!

SOC uncertainty single-arm two-arm simulation plotting boundaries
postprob ✔️
postprobDist ✔️ ✔️
predprob ✔️
predprobDist ✔️ ✔️
ocPostprob ✔️ ✔️
ocPostprobDist ✔️ ✔️ ✔️
ocPredprob ✔️ ✔️
ocPredprobDist ✔️ ✔️ ✔️
ocRctPostprobDist ✔️ ✔️ ✔️ ✔️
ocRctPredprobDist ✔️ ✔️ ✔️ ✔️
plotBeta ✔️ ✔️
plotDecision ✔️
plotOc ✔️
plotBounds ✔️
boundsPostprob ✔️
boundsPredprob ✔️

Concluding remarks



phase1b can be helpful to many therapeutic areas that use binary endpoint if beta priors are appropriate

Big thank you to Daniel Sabanés Bové for mentorship. Roche colleagues Isaac Gravestock, John Kirkpatrick, Craig Gower-Paige et al who collaborated and supported.

Issue page

Let’s connect

Code for this presentation

Next stop : ISCB46 & RoES Graz

License info

Please acknowledge authors and creators


Creative Common License used

For phase1b see author list

For this presentation, Audrey Yeo

References

  • Thall P F, Simon R (1994), Practical Guidelines for Phase IIB Clinical Trials, Biometrics, 50, 337-349

  • Lee J J, Liu D D (2008), A Predictive probability design for phase II cancer clinical trials, 5(2), 93-106, Clinical Trials

  • Yeo, A T, Sabanés Bové D, Elze M, Pourmohamad T, Zhu J, Lymp J, Teterina A (2024). Phase1b : Calculations for decisions on Phase 1b clinical trials. R package version 1.0.0, https://genentech.github.io/phase1b

  • Inclusive Speaker Orientation Linux Foundation

Some more references

  • Zeileis, Fisher, Hornik, Ihaka, McWhite, Murrell, Stauffer, Wilke (2020). colorspace: A Toolbox for Manipulating and Assessing Colors and Palettes. Journal of Statistical Software.

  • Pollock et al (2020). Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. The New England Journal of Medicine. Vol. 383. No. 27, doi: 10.1056/NEJMoa203457

  • Roychoudhury, S (2022) A Bayesian Group-sequential Design for COVID-19 Vaccine Development, DIA BSWG F2F Meeting, Joint Statistician Meeting, Washington DC August 9th, 2022

Backup slides

Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine

\[ \theta = \frac{1-VE}{2-VE} \]

\[ VE = (1-2\theta) * (1-\theta) \]

where case rate = \(\theta\) and vaccine efficacy = \(VE\)

\[ H_{o} : p = Pr( VE ≤ 30 \% \ | \ data, prior) \]

\[ H_{a} : p = Pr(VE > 30 \% \ | \ data, prior) \] Prior is \(Beta(0.700102, 1)\) which corresponds to

\[ \mu (\theta = case \ rate \ ratio) = \frac{0.700102}{1.700123} \approx 0.411 \]

\[ = H_{a} : p = Pr( \theta ≤ 0.4117647 \ | \ data, prior) \]

Efficacy criteria :

Interim : \[ p > 99.50 \% \] Final: \[ p > 99.50 \% \]

Strength of Priors (CDF version)

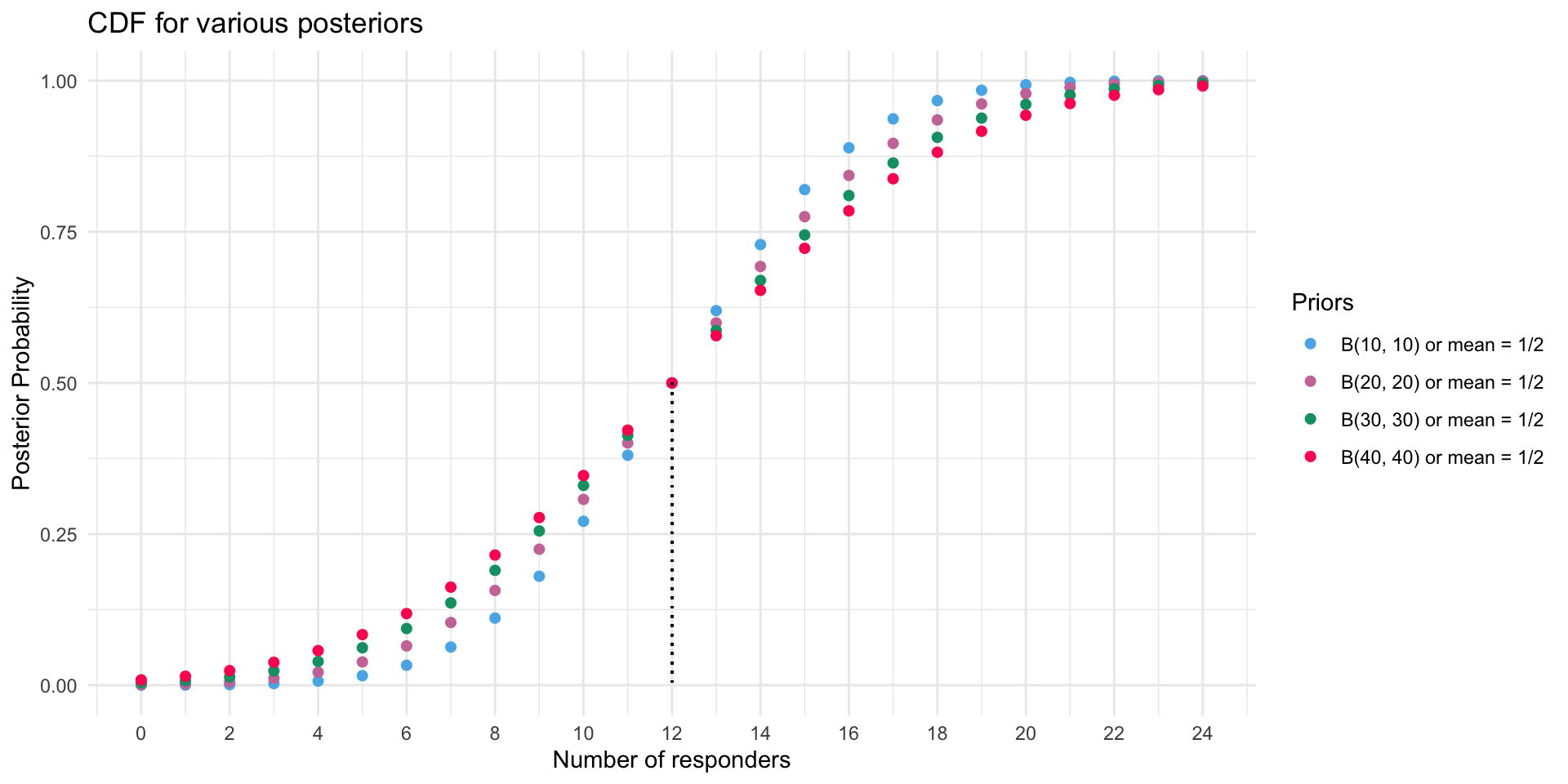
Strength of Priors on Predictive Posteriors (CDF version)

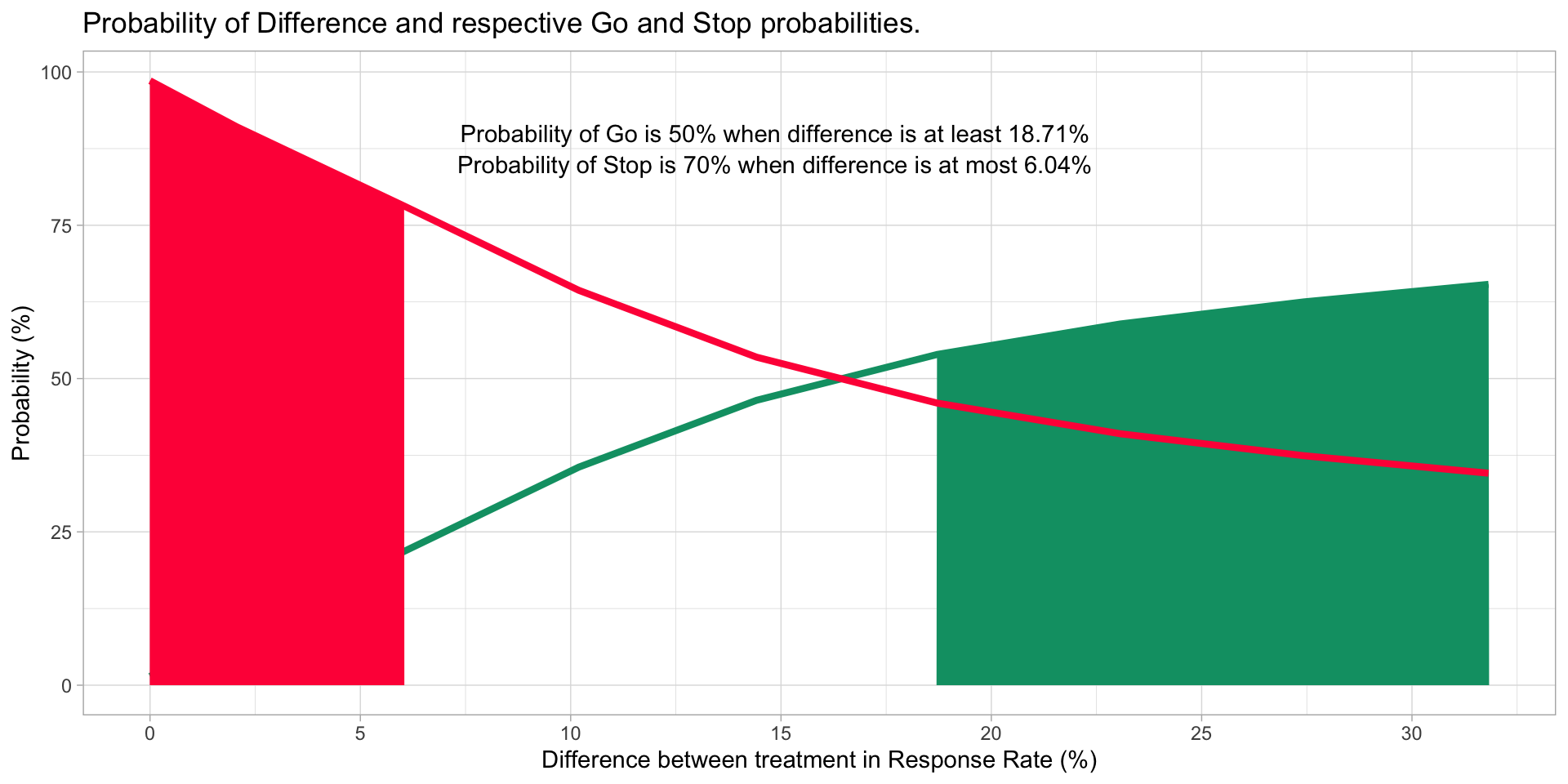
Evaluating the difference between two arms ?

Meaningful improvement if \[ \Delta > 15\% \ when \ \Delta = \pi_{E} - \pi_{S}\]

Efficacious if \[ Pr( \Delta > 15 \% | data ) > 70\% \ otherwise \ Pr( \Delta < 15 \% | data ) > 70\% \]

Standard of Care Distribution when unknown, ...Dist series:

Concerning:

  • postprobDist()
  • predprobDist
  • ocPostprobDist()
  • ocPredprobDist()

Using the approach by Thall and Simon (Biometrics, 1994), this evaluates the posterior probability of achieving superior response rate in the treatment group E compared to standard of care S.

  • The desired improvement is denoted as delta. There are two options in using delta. The absolute case when relativeDelta = FALSE and relative as when relativeDelta = TRUE.

Standard of Care Distribution when unknown, ...Dist series continued :

Desired improvement delta, two approaches:

  1. The absolute case is when we define an absolute delta, greater than P_S, the response rate of the standard of care or control or S group such that the posterior is Pr(P_E > P_S + delta | data).

  2. In the relative case, we suppose that the treatment group’s response rate is assumed to be greater than P_S + (1-P_S) * delta such that the posterior is Pr(P_E > P_S + (1 - P_S) * delta | data).

In summary:

  1. relativeDelta = FALSE: Pr(P_E > P_S + delta | data)

  2. relativeDelta = TRUE : Pr(P_E > P_S + (1 - P_S) * delta | data)

Predictive posterior probability for Decision 1

Concerning:

  • predprobDist
  • ocPredprobDist()
  • ocRctPredprobDist()

Predictive posterior probability for Decision 1:

When decision1 = TRUE, criteria for Decision 1 for Interim looks are :

  • Interim GO : P( success at final) > phiU

  • Interim STOP : P( success at final) < phiL

When decision1 = TRUE, criteria for Decision 1 for Final looks are:

  • Final GO : P( response rate > p0 | data) > tT

  • Final STOP : P( response rate > p0 | data ) < tT

Predictive posterior probability for Decision 2

Still concerning:

  • predprobDist
  • ocPredprobDist()
  • ocRctPredprobDist()

When decision1 = FALSE, criteria for Decision 2 for Interim looks are :

  • Interim GO : P ( success at final) > phiU

  • Interim STOP : P (failure at final ) > phiFu

When decision1 = FALSE, criteria for Decision 2 for Final looks are :

  • Final GO : P( response rate > p0 | data) > tT

  • Final STOP : P( response rate < p1 | data) > tF

Posterior probability

Concerning:

  • postprobDist()
  • ocPostprobDist()
  • ocRctPostprobDist()

At final, the criteria are:

  • Final GO : Pr( response rate > p1 | data) > tU

  • Final STOP : Pr( response rate < p0 | data) > tL